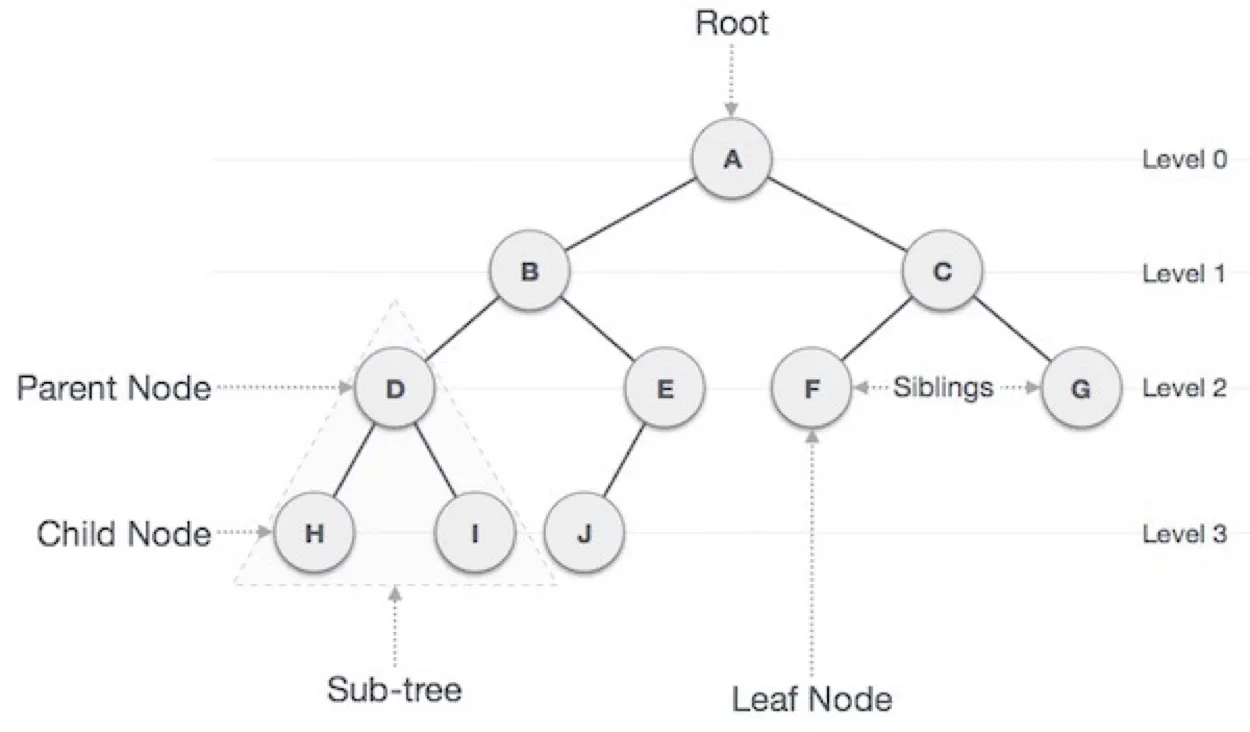
트리는 그래프 중 하나로 그래프의 특징처럼 정점과 간선으로 이루어져있고, 트리 구조로 배열된 계층적 데이터의 집합이다.
구성
루트노드 : 가장 위에 있는 노드
내부노드 : 루트노드와 내부노드 사이에 있는 노드로 리프노드를 제외한 노드
리프노드 : 자식이 없는 노드
특징
•
데이터를 순차적으로 저장하지 않기 때문에 비선형 자료구조
•
트리내에 또 다른 트리가 있는 재귀적 자료구조
•
단순 순환(Loop)을 갖지 않고, 연결된 무방향 그래프 구조
•
노드 간에 부모 자식 관계를 갖고 있는 계층형 자료구조이며 모든 자식 노드는 하나의 부모 노드만 가진다.
트리의 높이와 레벨
깊이 : 루트노드부터 특정노드까지 최단 거리로 갔을 때의 거리
높이 : 루트노드부터 리프노드까지 거리중 가장 긴 거리
레벨 : 주어지는 문제마다 다르지만 보통 깊이와 같은 의미
서브트리 : 트리 내의 하위 집합
이진 트리
자식의 노드 수가 두개 이하인 트리를 의미
•
정이진 트리 : 자식노드가 0 또는 2개인 이진 트리
•
완전 이진 트리 : 왼쪽부터 채워져 있는 이진 트리를 의미하며 마지막 레벨을 제외한 모든 레벨이 채워져 있고 왼쪽부터 채워져 있다.
•
변질 이진 트리 : 자식 노드가 하나밖에 없는 이진 트리
•
포화 이진 트리 : 모든 노드가 꽉 차 있는 이진 트리
•
균형 이진 트리 : 왼쪽과 오른쪽의 노드의 높이 차이가 1 이하인 이진 트리
이진 탐색 트리
이진 탐색 트리(BST) 노드의 오른쪽 하위 트리에 노드 값보다 큰값이 있는 노드만 포함되고 왼쪽 하위 트리에는 노드 값보다 작은 값이 들어있는 트리, 검색에 용이하지만 트리 삽입 순서에 따라 선형적일수 있고 이 최악의 경우 삽입, 삭제, 탐색 모두 O(n)이다.
AVL 트리
앞서 설명한 최악의 경우인 선형적인 트리가 되는 것을 방지하고 스스로 균형을 잡는 이진 탐색 트리이다.
레드 블랙 트리
균형 이진 탐색 트리로 탐색, 삽입, 삭제 모두 시간 복잡도가 O(logn)이다. 각 노드에 빨간색 혹은 검은색의 색상을 나타내는 추가 비트를 저장하며, 삽입 및 삭제 중에 트리가 균형을 유지하는데 사용된다.
모든 리프노드와 루트노드는 블랙이고 어떤 노드가 레드이면 그 노드의 자식은 반드시 블랙이다.