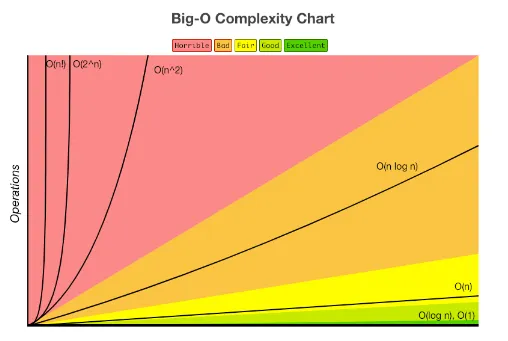
시간복잡도란?
•
알고리즘이 문제를 해결하는데 걸리는 시간이 얼마나 되는지를 나타내는 척도
시간복잡도의 중요성
•
알고리즘의 효율성을 평가하는 기준
•
동일한 문제를 해결하는 다양한 알고리즘이 있을 때, 어떤 알고리즘이 더 빠르고 효율적인지 판단할 수 있다.
시간복잡도 표현방법
•
최상의 경우 : 오메가 표기법 (Big-Ω Notation)
•
평균의 경우 : 세타 표기법 (Big-θ Notation)
•
최악의 경우 : 빅오 표기법 (Big-O Notation)
※ 알고리즘이 복잡해질수록 평균적인 경우는 구하기가 매우 어려워 지기 때문에 최악의 경우로 알고리즘 성능을 파악한다.
빅오 표기법(Big - O)
•
불필요한 연산을 제거하여 알고리즘 분석을 쉽게 할 목적으로 사용된다.
•
Big - O 로 측정되는 복잡성에는 시간복잡도와 공간복잡도가 있다.
◦
시간복잡도
▪
입력된 N의 크기에 따라 실행되는 조작의 수
◦
공간복잡도
▪
알고리즘이 실행될 때 사용하는 메모리의 양
▪
요즘은 데이터를 저장할 수 있는 메모리의 발전으로 중요도가 낮아졌다.
•
실행시간이 아닌 연산횟수 수치로 판별하는 이유는?
◦
실행시간은 컴퓨터의 하드웨어 또는 프로그래밍 언어에 따라 편차가 있기 때문에 명령어의 연산 횟수를 나타낸다.
시간복잡도 단계 (빠른 순)
O(1) → O(logn) → O(n) → O(nlogn) → O(n^2)
•
O(1) - 상수 시간
◦
문제를 해결하는데 오직 한 단계만 처리함.
◦
일정한 복잡도, 입력값이 증가하더라도 시간이 늘어나지 않는다.
◦
배열에서 원소 하나를 찾는 예시
public static int getFirst(int[] nums) {
return nums[0];
}
Java
복사
•
O(logn) - 로그 시간
◦
문제를 해결하는데 필요한 단계들이 연산마다 특정 요인에 의해 줄어듬.
◦
이진 탐색 알고리즘의 예시
▪
입력 크기가 증가함에 따라 실행 시간이 로그함수의 형태로 증가한다.
▪
정렬된 배열에서 특정 값을 찾을 때 유용하게 사용된다.
public static int binarySearch(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) {
return mid;
} else if (nums[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return -1;
}
Java
복사
•
O(n) - 선형 시간
◦
문제를 해결하기 위한 단계의 수와 입력값 n이 1:1 관계를 가짐.
◦
입력값이 증가함에 따라 시간 또한 같은 비율로 증가한다.
◦
입력한 배열을 역순으로 만드는 함수를 구현한 예시
public static int[] reverse(int[] nums) {
int[] reversed = new int[nums.length];
for (int i = 0; i < nums.length; i++) {
reversed[nums.length - i - 1] = nums[i];
}
return reversed;
Java
복사
•
O(nlogn) - 선형 로그 시간
◦
문제를 해결하기 위한 단계의 수가 N*(log2N) 번 만큼의 수행시간을 가진다.
◦
병합 정렬을 이용해 정렬하는 예시
public static void mergeSort(int[] nums, int left, int right) {
if (left < right) {
int mid = left + (right - left) / 2;
mergeSort(nums, left, mid);
mergeSort(nums, mid + 1, right);
merge(nums, left, mid, right);
}
}
Java
복사
•
O(n^2) - 2차 시간
◦
문제를 해결하기 위한 단계의 수는 입력값 n의 제곱.
◦
입력값이 증가함에 따라 시간이 n의 제곱수의 비율로 증가하는 것을 의미
◦
정수의 배열을 선택 정렬을 이용해 정렬하는 예시
public static void selectionSort(int[] nums) {
for (int i = 0; i < nums.length - 1; i++) {
int minIdx = i;
for (int j = i + 1; j < nums.length; j++) {
if (nums[j] < nums[minIdx]) {
minIdx = j;
}
}
int tmp = nums[i];
nums[i] = nums[minIdx];
nums[minIdx] = tmp;
}
}
Java
복사
•
O(2^n) - 지수 시간
◦
기하급수적 복잡도라 부르며 상수의 n제곱만큼 늘어나는 수행시간
◦
피보나치수열을 구하는 예시
public static int fibonacci(int n) {
if (n <= 1) {
return n;
}
return fibonacci(n - 1) + fibonacci(n - 2);
}
Java
복사